Esfera

INTRODUÇÃO A ESFERA

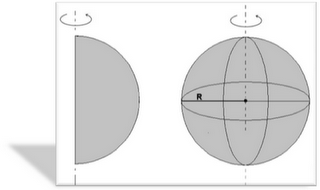
A esfera é um sólido limitado por uma superfície curva de revolução que tem todos os pontos igualmente distantes de um ponto interior chamado centro. A superfície esférica é resultado da revolução de uma semicircunferência em torno do diâmetro.

Superfície esférica: é o conjunto dos pontos do espaço que equidistam de um ponto fixo.

Esfera: é a união dos pontos da superfície esférica com todos os pontos da região interna a esta.

Elementos de uma esfera

Eixo (e) – É a reta que passa pelo centro da esfera.

Pólos( P e Q) – São as intersecções da superfície esférica com o eixo.

Equador: É a circunferência que tem se centro coincidente com o centro da esfera e é perpendicular ao seu eixo

Paralelo: É toda a circunferência sobre a superfície esférica que é paralela ao equador.

Meridianos: É toda a circunferência sobre a superfície esférica que passa pelos pólos P e Q

Seção de uma esfera

Toda seção plana de uma esfera é um círculo cujo centro é a interseção do plano secante com o diâmetro da esfera perpendicular a ele. Se o plano passa pelo centro da esfera, a seção será um círculo máximo; e nos demais casos, a cortará segundo um círculo menor, podendo ser reduzido a um ponto no caso do plano ser tangente à esfera.

R_e = raio da esfera

d = Distância do centro da esfera ao centro da secção

r= raio da secção da esfera

Área de uma superfície esférica
A área de uma superfície esférica de raio  r é igual a 4 r². 

Volume da esfera 
 Por ser considerada um sólido geométrico, a esfera possui volume representado pela seguinte equação:

     

Fuso esférico

Se uma circunferência com extremidades num eixo α ( 0° < α ≤ 360° ) gira em torno do eixo, ela gera uma superfície que é chamada fuso esférico

Fuso esférico é a parte da superfície esférica compreendida entre dois de seus círculos máximos.

Cunha esférica

Se um semicírculo com diâmetro num eixo gira em graus (0° < α ≤ 360°) em torno do eixo, ele gera um solido que é chamado de cunha esférica.

A Cunha esférica é a parte da esfera compreendida entre dois de seus círculos máximos.

A esfera possui inúmeras aplicações, como exemplo podemos citar a Óptica (Física), a seção de uma esfera forma uma lente esférica, que são objetos importantes na construção de óculos. Corpos esféricos possuem grande importância na Engenharia Mecânica, a parte interior de inúmeras peças capazes de realizar movimentos circulares sobre eixos é constituída de esferas de aço. Um bom exemplo dessas peças é o rolamento. 

EXERCÍCIOS RESOLVIDOS

11-      Uma secção feita numa esfera por um plano alfa é um círculo de perímetro 2 π cm. A distância do centro da esfera ao plano alfa é 2 raiz de 2 cm. Calcule a medida r do raio da esfera.

Resposta: se o comprimento (ou perímetro do circulo) é igual a 2 . π, então:
raio( r ) 2 . π . r = 2 . π
r = 1cm

Calculamos o raio da secção. Agora para calcular o raio ( R ) da esfera, devemos usar o teorema de Pitágoras relacionando o raio da secção, raio da esfera e a distância entre o centro da esfera e o plano alfa que secciona a esfera.

R² = 1² + (2 . raiz de 2)²
R² = 1 + 4 . 2
R² = 9
R = 3 cm

22-     Um plano alfa secciona uma esfera de raio 20cm. A distância do centro da esfera ao plano alfa é 12cm. Calcule a área da secção obtida.

Resposta: igualmente ao exercício acima, devemos aplicar a fórmula de Pitágoras:
20² = 12² + r²
r² + 144 = 400
r² = 256
r = 16 cm
O exercício pede a área da secção, que é um circulo. Logo temos:
16² . π = 256 . π cm²

3-     Dois cubos de metal, de aresta π* cm e 2π cm, fundem-se para formar uma esfera. Qual o comprimento do raio dessa esfera?

Resposta: O volume dessa nova esfera será igual a soma dos volumes dos cubos:
Cubo 1 = Volume1 = π³
Cubo 2 = Volume2 = (2π)³ = 8π³
V1 + V2 = π³ + 8π³ => 9π³
O volume de uma esféra é dado por: 4πR³/3 , aonde R = raio.
9π³ = 4πR³/3
27π³/4π = R³
R = ³V(27π²/4)

44-     O volume de uma esfera A é 1/8 do volume de uma esfera B. Se o raio da esfera B mede 10, então quanto mede o raio da esfera A?

Resposta:

Va = Vb/8
4πR³/3 = 4π(10)³/3(8)
4πR³ = 4π(10)³/8
R³ = 10³/2³
R = 10/2

 R = 5

55-     Um cilindro eqüilátero de volume V encontra- se cheio de água, quando uma esfera, cujo o raio coincide com o raio da base do cilindro, é mergulhada completamente no cilindro fazendo transbordar certa quantidade de água. Qual o volume de água restante no cilindro em função de V?

Resposta: é o volume que o cilindro tem menos o da esfera:
Volume restante: r²π2r - 4πr³/3
Volume restante: (6πr³ - 4πr³)/3
Volume restante: 2πr³/3

Ali está em função do raio, mas podemos igualar o raio a:
v = r²π2r (volume do cilindro)... isolando o raio...
v = 2πr³
r³ = v/2π
r = ³V(v/2π)
Substituindo o valor do raio:
Volume restante: 2π[³V(v/2π)]³/3
Volume restante: v/3

EXERCÍCIO DE FIXAÇÃO

1) Deseja-se construir um reservatório de água na forma de uma semi-esfera, em um terreno de dimensões 30 m por 40 m. O reservatório deverá ocupar 30% da área deste terreno. Calcule o volume de água em litros que poderão ser armazenados neste reservatório.

2) Calcule o volume de uma esfera inscrita em um cubo de área lateral igual a 64 m².

3) Encontre a relação entre o raio de uma esfera e a altura de um cilindro eqüilátero sabendo  que a área total do cilindro é igual à da esfera.

4) Calcular a área de uma esfera sabendo que o perímetro do hexágono regular inscrito em um de seus círculos máximos mede 30 cm.

5) Calcular o volume de uma esfera circunscrita a um cone eqüilátero cuja altura mede 16 dm.

6) Um cilindro circular reto tem sua superfície total equivalente à superfície lateral de um prisma oblíquo cuja secção reta é um pentágono regular de lado igual a 3 m e a aresta lateral, 4/3 m. Sabe-se que o perímetro da secção meridiana do cilindro vale 14 m. Qual o raio da base do cilindro?

      

7) Considere um retângulo, de altura y e base x, com x>y, e dois semicírculos com centros nos lados do retângulo. Calcule o volume do sólido obtido pela rotação da região sombreada em torno de um eixo que passa pelos centros dos semicírculos.

  

8) Uma esfera de raio 10 cm é interceptada por um plano que dista 6cm de seu centro. Qual o comprimento da circunferência gerada pela interseção?

9) Uma laranja de 12 gomos iguais assemelha-se a uma esfera de raio R. Qual a área da superfície total de cada gomo?

10) Um cubo de aresta 10 cm tem os quatro vértices A, B, C e D de uma de suas faces, F, sobre a superfície de uma esfera S de raio r. Sabendo que a face oposta a F é tangente à esfera S no ponto P, calcule o raio r.

11) Duas esferas de raio r foram colocadas dentro de um cilindro circular reto com altura 4r, raio da base r e espessura desprezível. Calcule a razão entre o volume do cilindro não ocupado pelas esferas e o volume das esferas.

12) Determine a razão entre os volume de uma esfera de raio R e o de um cubo nela inscrito.